面试准备 嘤嘤嘤
Python
Python相关面试知识点
JS
== 和 === 区别:
== 代表相同, ===代表严格相同
当进行双等号比较时候: 先检查两个操作数数据类型,如果相同, 则进行===比较, 如果不同, 则愿意为你进行一次类型转换, 转换成相同类型后再进行比较, 而===比较时, 如果类型不同,直接就是false.
switch-case中使用===
NaN 只能用 isNaN() 来判断
null 和 undefined
undefined表示未初始化的值,类型是undefined
null 表示一个不存在的对象,类型是object
nan的类型是number?
数据类型
值类型(基本类型):字符串(String)、数字(Number)、布尔(Boolean)、对空(Null)、未定义(Undefined)、Symbol。
引用数据类型:对象(Object)、数组(Array)、函数(Function)。
js 正则表达式
| 修饰符 | 描述 |
|---|---|
| i | 执行对大小写不敏感的匹配。 |
| g | 执行全局匹配(查找所有匹配而非在找到第一个匹配后停止)。 |
| m | 执行多行匹配。 |
test() 方法用于检测一个字符串是否匹配某个模式,如果字符串中含有匹配的文本,则返回 true,否则返回 false。
exec() 方法用于检索字符串中的正则表达式的匹配。 该函数返回一个数组,其中存放匹配的结果。如果未找到匹配,则返回值为 null。
this 关键字
面向对象语言中 this 表示当前对象的一个引用。 但在 JavaScript 中 this 不是固定不变的,它会随着执行环境的改变而改变。
- 在方法中,this 表示该方法所属的对象。
- 如果单独使用,this 表示全局对象。
- 在函数中,this 表示全局对象。
- 在函数中,在严格模式下,this 是未定义的(undefined)。
- 在事件中,this 表示接收事件的元素。
- 类似 call() 和 apply() 方法可以将 this 引用到任何对象。
计算机网络
HTTP 状态码
500 Internal Server Error 服务器内部错误,无法完成请求
502 Bad Gateway 作为网关或者代理工作的服务器尝试执行请求时,从远程服务器接收到了一个无效的响应
403 Forbidden 服务器理解请求客户端的请求,但是拒绝执行此请求
404 Not Found 服务器无法根据客户端的请求找到资源(网页)。通过此代码,网站设计人员可设置"您所请求的资源无法找到"的个性页面
401 Unauthorized 请求要求用户的身份认证
301 Moved Permanently 永久移动。请求的资源已被永久的移动到新URI,返回信息会包括新的URI,浏览器会自动定向到新URI。今后任何新的请求都应使用新的URI代替
302 Found 临时移动。与301类似。但资源只是临时被移动。客户端应继续使用原有URI
200 OK 请求成功。一般用于GET与POST请求
OSI 7层结构
应用层:文件传输,常用协议HTTP,snmp,FTP ,
表示层:数据格式化,代码转换,数据加密,
会话层:建立,解除会话
传输层:提供端对端的接口,tcp,udp
网络层:为数据包选择路由,IP,icmp
数据链路层:传输有地址的帧
物理层:二进制的数据形式在物理媒体上传输数据
常考题
- TCP三次握手(为什么不能两次)、四次挥手
技术栈
前端
- js
- Vuejs
NPM(只是用过,不知道)- Redis 原理等
- WebSocket 原理
机器学习
特征工程-标准化和归一化
基本上两种说法混用
- z-score标准化:特征就变成了均值为0,方差为1了
- max-min标准化:特征值映射到[0,1]之间
- mean标准化(中心化):特征值映射到[-1,1]之间
- L1/L2范数标准化:统一量纲
特征工程-异常特征样本清洗
- 第一种是聚类,比如我们可以用KMeans聚类将训练样本分成若干个簇,如果某一个簇里的样本数很少,而且簇质心和其他所有的簇都很远,那么这个簇里面的样本极有可能是异常特征样本了。我们可以将其从训练集过滤掉。
- 第二种是异常点检测方法,主要是使用iForest或者one class SVM,使用异常点检测的机器学习算法来过滤所有的异常点。
特征工程-不平衡数据的处理方法
- 对较多的那个类别进行欠采样(under-sampling),舍弃一部分数据,使其与较少类别的数据相当
- 对较少的类别进行过采样(over-sampling),重复使用一部分数据,使其与较多类别的数据相当
- 阈值调整(threshold moving),将原本默认为0.5的阈值调整到较少类别/(较少类别+较多类别)即可
在第一种方法中,我们浪费了很多数据。而第二类方法中有无中生有或者重复使用了数据,会导致过拟合的发生。
聚类的几种方法
数据科学中必须熟知的5种聚类算法 (opens new window)
深度学习
Machine_Learning_Resources (opens new window)
回归问题:损失函数/性能标准
均方误差(MAE):欧式距离的平方的平均
L1损失函数和L2损失函数:
L2损失函数对异常点比较敏感,因为L2将误差平方化,使得异常点的误差过大,模型需要大幅度的调整,这样会牺牲很多正常的样本。
而L1损失函数由于导数不连续,可能存在多个解,当数据集有一个微笑的变化,解可能会有一个很大的跳动,L1的解不稳定。
分类问题:损失函数/性能标准
交叉熵:刻画的是两个概率分布之间的距离,
softmax+cross-entropy loss 擅长于学习类间的信息,因为它采用了类间竞争机制,它只关心对于正确标签预测概率的准确性,忽略了其他非正确标签的差异,导致学习到的特征比较散。
L-Softmax loss、A-Softmax loss、CosFace、ArcFace、COCO loss、Angular Triplet Loss等都是angular margin learning系列
- Softmax loss无法确保类内的紧凑和类间的疏离。
- L-Softmax:Large Margin Softmax Loss(简称L-Softmax loss),其主要思想是在标准的Softmax loss中加入了一个角度约束,确保不同类别的样本分界更明显。
- A-Softmax的权重归一化了(Spherenet)
Triplet loss
- 输入是一个三元组
<a, p, n>- a: anchor
- p: positive, 与 a 是同一类别的样本
- n: negative, 与 a 是不同类别的样本
所以最终的优化目标是拉近 a, p 的距离, 拉远 a, n 的距离
easy triplets:
hard triplets:
semi-hard triplets:
训练方法:Online
从训练集中抽取 B 个样本,然后计算 B 个embeddings,可以产生
<a, p, n>)
- 输入是一个三元组
正则化:
神经网络模型
- VGG/GoogleNet/Resnet
- 注意力机制
图像识别
目标检测:标准
Linux
Linux 、操作系统
| 编号 | 信号名称 | 内容 |
|---|---|---|
| 2 | SIGINT | 进程终端,CTRL+C |
| 15 | SIGTEM | 请求中断,kill默认 |
| 9 | SIGKILL | 强制中断 |
| 20 | SIGSTOP | 停止(挂起不退出)进程 CRTL+Z |
Unix进程间通信方式(IPC)
管道(Pipe):管道可用于具有亲缘关系进程间的通信,允许一个进程和另一个与它有共同祖先的进程之间进行通信。
命名管道(named pipe):命名管道克服了管道没有名字的限制,因此,除具有管道所具有的功能外,它还允许无亲缘关系进程间的通信。命名管道在文件系统中有对应的文件名。命名管道通过命令mkfifo或系统调用mkfifo来创建。
信号(Signal):信号是比较复杂的通信方式,用于通知接受进程有某种事件发生,除了用于进程间通信外,进程还可以发送信号给进程本身;linux除了支持Unix早期信号语义函数sigal外,还支持语义符合Posix.1标准的信号函数sigaction(实际上,该函数是基于BSD的,BSD为了实现可靠信号机制,又能够统一对外接口,用sigaction函数重新实现了signal函数)。
消息(Message)队列:消息队列是消息的链接表,包括Posix消息队列system V消息队列。有足够权限的进程可以向队列中添加消息,被赋予读权限的进程则可以读走队列中的消息。消息队列克服了信号承载信息量少,管道只能承载无格式字节流以及缓冲区大小受限等缺
共享内存:使得多个进程可以访问同一块内存空间,是最快的可用IPC形式。是针对其他通信机制运行效率较低而设计的。往往与其它通信机制,如信号量结合使用,来达到进程间的同步及互斥。
内存映射(mapped memory):内存映射允许任何多个进程间通信,每一个使用该机制的进程通过把一个共享的文件映射到自己的进程地址空间来实现它。
信号量(semaphore):主要作为进程间以及同一进程不同线程之间的同步手段。
套接口(Socket):更为一般的进程间通信机制,可用于不同机器之间的进程间通信。起初是由Unix系统的BSD分支开发出来的,但现在一般可以移植到其它类Unix系统上:Linux和System V的变种都支持套接字。
常用命令
- kill 与 kill -9 的区别: kill 发送 SIGTERM -9 发送 SIGKILL (opens new window)
计算机指令执行过程
- 取指令阶段
- 取指令(Instruction Fetch,IF)阶段是将一条指令从主存中取到指令寄存器的过程。
- 程序计数器PC中的数值,用来指示当前指令在主存中的位置。当一条指令被取出后,PC中的数值将根据指令字长度而自动递增:若为单字长指令,则(PC)+1=PC;若为双字长指令,则(PC)+2=PC,依此类推。
//PC -> AR -> Memory //Memory -> IR - 指令译码阶段
- 取出指令后,计算机立即进入指令译码(Instruction Decode,ID)阶段。
- 在指令译码阶段,指令译码器按照预定的指令格式,对取回的指令进行拆分和解释,识别区分出不同的指令类别以及各种获取操作数的方法。
- 在组合逻辑控制的计算机中,指令译码器对不同的指令操作码产生不同的控制电位,以形成不同的微操作序列;在微程序控制的计算机中,指令译码器用指令操作码来找到执行该指令的微程序的入口,并从此入口开始执行。
// { 1.Ad //Memory -> IR -> ID -> { 2.PC变化 // { 3.CU(Control Unit) - 访存取数阶段
- 根据指令需要,有可能要访问主存,读取操作数,这样就进入了访存取数(Memory,MEM)阶段。
- 此阶段的任务是:根据指令地址码,得到操作数在主存中的地址,并从主存中读取该操作数用于运算。
//Ad -> AR -> AD -> Memory - 执行指令阶段
- 在取指令和指令译码阶段之后,接着进入执行指令(Execute,EX)阶段。
- 此阶段的任务是完成指令所规定的各种操作,具体实现指令的功能。为此,CPU的不同部分被连接起来,以执行所需的操作。
- 例如,如果要求完成一个加法运算,算术逻辑单元ALU将被连接到一组输入和一组输出,输入端提供需要相加的数值,输出端将含有最后的运算结果。
//Memory -> DR -> ALU - 结果写回阶段
- 作为最后一个阶段,结果写回(Writeback,WB)阶段把执行指令阶段的运行结果数据“写回”到某种存储形式:结果数据经常被写到CPU的内部寄存器中,以便被后续的指令快速地存取;在有些情况下,结果数据也可被写入相对较慢、但较廉价且容量较大的主存。许多指令还会改变程序状态字寄存器中标志位的状态,这些标志位标识着不同的操作结果,可被用来影响程序的动作。
//DR -> Memory - 循环阶段
- 在指令执行完毕、结果数据写回之后,若无意外事件(如结果溢出等)发生,计算机就接着从程序计数器PC中取得下一条指令地址,开始新一轮的循环,下一个指令周期将顺序取出下一条指令。
//重复 1~5 //遇hlt(holt on)停止
编译步骤
编译预处理
读取c源程序,对其中的伪指令(以#开头的指令)和特殊符号进行处理
编译阶段
经过预处理得到的输出文件中,将只有常量。如数字、字符串、变量的定义,以及C语言的关键字,如main,if,else,for,while,{,},+,-,*,\,等等。编译程序所要作得工作就是通过词法分析和语法分析,在确认所有的指令都符合语法规则之后,将其翻译成等价的中间代码表示或汇编代码。
优化阶段
优化处理是编译系统中一项比较艰深的技术。它涉及到的问题不仅同编译技术本身有关,而且同机器的硬件环境也有很大的关系。优化一部分是对中间代码的优化。这种优化不依赖于具体的计算机。另一种优化则主要针对目标代码的生成而进行的。
汇编过程
汇编过程实际上指把汇编语言代码翻译成目标机器指令的过程。对于被汇编系统处理的每一个C语言源程序,都将最终经过这一处理而得到相应的目标文件。目标文件中所存放的也就是与源程序等效的目标的机器语言代码。
链接程序
由汇编程序生成的目标文件并不能立即就被执行,其中可能还有许多没有解决的问题。例如,某个源文件中的函数可能引用了另一个源文件中定义的某个符号(如变量或者函数调用等);在程序中可能调用了某个库文件中的函数,等等。所有的这些问题,都需要经链接程序的处理方能得以解决。
微内核与宏内核:
它们的区别是微内核有用户态的驱动程序和系统服务 微内核与宏内核 (opens new window)
- 宏内核: Linux、Windows,
- 优点为操作系统的调用非常快,效率高,缺点是安全性不足
- 微内核: Minix、Fuchsia、鸿蒙,
- 优点为异构化、安全性高,缺点是效率很低
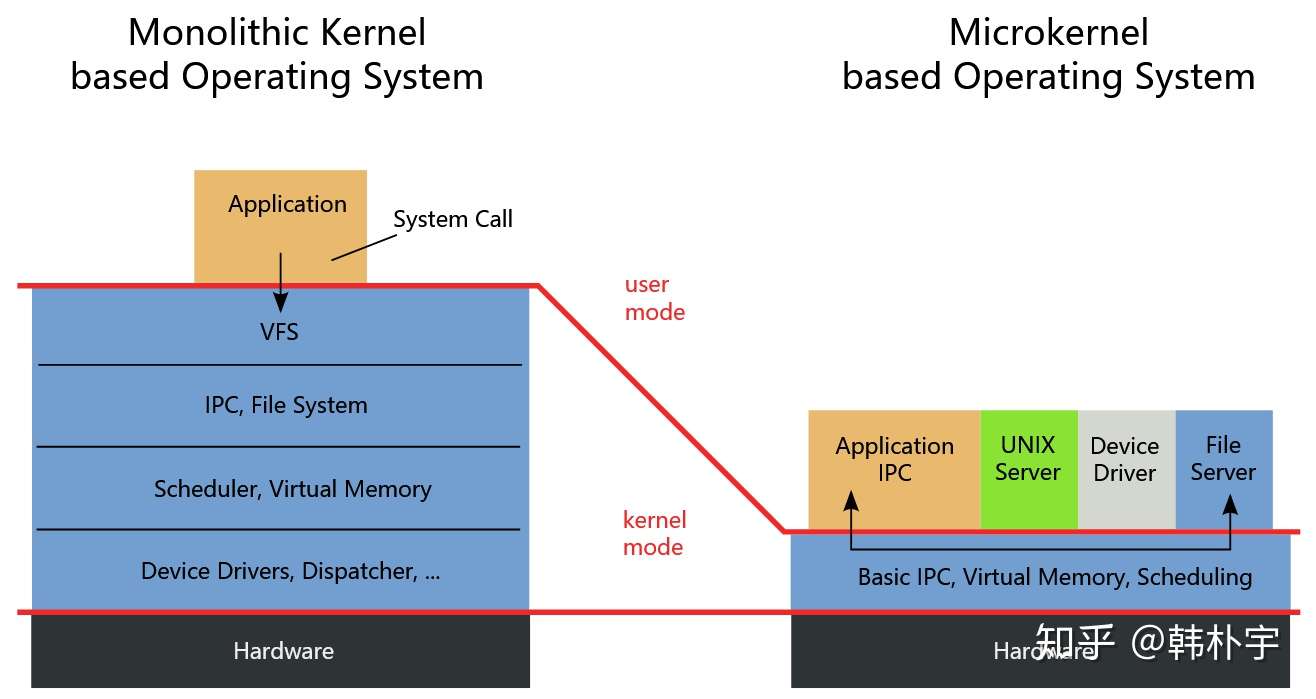
宏内核的过程: 网卡发来中断, CPU执行网卡驱动设置的处理程序,要求网卡使用DMA将数据存到内核中,然后返回.DMA完成后,再次中断,系统的IP子系统分析已经存储的IP数据报,确定是TCP数据,根据端口号唤醒正在等待recv()的浏览器,将数据复制到recv参数里的缓冲区. 整个过程只发生一次数据的复制,两次中断.
微内核的过程: 网卡发来中断, CPU执行HAL设置的处理程序, HAL确定这个中断应该被/bin/e1000d这个进程处理,于是唤醒/bin/e1000d, 把网卡发来的中断信息发给/bin/e1000d, e1000d将“写网卡内存映射的寄存器.....要求网卡进行DMA..."这种消息发给内核,内核收到之后执行,然后DMA结束之后把内存数据复制给e1000d,e1000d处理之后使用IPC把IP数据报发送给/bin/ipd,ipd处理后把TCP数据发送给浏览器。
数据库
1 事务
数据库事务(Database Transaction) ,是指作为单个逻辑工作单元执行的一系列操作,要么完全地执行,要么完全地不执行。 彻底理解数据库事务: http://www.hollischuang.com/archives/898
2 数据库索引
推荐: http://tech.meituan.com/mysql-index.html
MySQL索引背后的数据结构及算法原理 (opens new window)
聚集索引,非聚集索引,B-Tree,B+Tree,最左前缀原理
3 Redis原理
搞懂这些Redis知识点 (opens new window) Redis常见面试题 (opens new window)
Redis是什么?
- 是一个完全开源免费的key-value内存数据库
- 通常被认为是一个数据结构服务器,主要是因为其有着丰富的数据结构 strings、map、 list、sets、 sorted sets
Redis数据库
通常局限点来说,Redis也以消息队列的形式存在,作为内嵌的List存在,满足实时的高并发需求。在使用缓存的时候,redis比memcached具有更多的优势,并且支持更多的数据类型,把redis当作一个中间存储系统,用来处理高并发的数据库操作
- 速度快:使用标准C写,所有数据都在内存中完成,读写速度分别达到10万/20万
- 持久化:对数据的更新采用Copy-on-write技术,可以异步地保存到磁盘上,主要有两种策略,一是根据时间,更新次数的快照(save 300 10 )二是基于语句追加方式(Append-only file,aof)
- 自动操作:对不同数据类型的操作都是自动的,很安全
- 快速的主--从复制,官方提供了一个数据,Slave在21秒即完成了对Amazon网站10G key set的复制。
- Sharding技术: 很容易将数据分布到多个Redis实例中,数据库的扩展是个永恒的话题,在关系型数据库中,主要是以添加硬件、以分区为主要技术形式的纵向扩展解决了很多的应用场景,但随着web2.0、移动互联网、云计算等应用的兴起,这种扩展模式已经不太适合了,所以近年来,像采用主从配置、数据库复制形式的,Sharding这种技术把负载分布到多个特理节点上去的横向扩展方式用处越来越多。
Redis缺点
- 是数据库容量受到物理内存的限制,不能用作海量数据的高性能读写,因此Redis适合的场景主要局限在较小数据量的高性能操作和运算上。
- Redis较难支持在线扩容,在集群容量达到上限时在线扩容会变得很复杂。为避免这一问题,运维人员在系统上线时必须确保有足够的空间,这对资源造成了很大的浪费。
4 乐观锁和悲观锁
悲观锁:假定会发生并发冲突,屏蔽一切可能违反数据完整性的操作
乐观锁:假设不会发生并发冲突,只在提交操作时检查是否违反数据完整性。
乐观锁与悲观锁的具体区别: http://www.cnblogs.com/Bob-FD/p/3352216.html
5 MVCC
全称是Multi-Version Concurrent Control,即多版本并发控制,在MVCC协议下,每个读操作会看到一个一致性的snapshot,并且可以实现非阻塞的读。MVCC允许数据具有多个版本,这个版本可以是时间戳或者是全局递增的事务ID,在同一个时间点,不同的事务看到的数据是不同的。
MySQL (opens new window)的innodb引擎是如何实现MVCC的
innodb会为每一行添加两个字段,分别表示该行创建的版本和删除的版本,填入的是事务的版本号,这个版本号随着事务的创建不断递增。在repeated read的隔离级别(事务的隔离级别请看这篇文章 (opens new window))下,具体各种数据库操作的实现:
- select:满足以下两个条件innodb会返回该行数据:
- 该行的创建版本号小于等于当前版本号,用于保证在select操作之前所有的操作已经执行落地。
- 该行的删除版本号大于当前版本或者为空。删除版本号大于当前版本意味着有一个并发事务将该行删除了。
- insert:将新插入的行的创建版本号设置为当前系统的版本号。
- delete:将要删除的行的删除版本号设置为当前系统的版本号。
- update:不执行原地update,而是转换成insert + delete。将旧行的删除版本号设置为当前版本号,并将新行insert同时设置创建版本号为当前版本号。
其中,写操作(insert、delete和update)执行时,需要将系统版本号递增。
由于旧数据并不真正的删除,所以必须对这些数据进行清理,innodb会开启一个后台线程执行清理工作,具体的规则是将删除版本号小于当前系统版本的行删除,这个过程叫做purge。
通过MVCC很好的实现了事务的隔离性,可以达到repeated read级别,要实现serializable还必须加锁。
6 MyISAM和InnoDB
MyISAM 适合于一些需要大量查询的应用,但其对于有大量写操作并不是很好。甚至你只是需要update一个字段,整个表都会被锁起来,而别的进程,就算是读进程都无法操作直到读操作完成。另外,MyISAM 对于 SELECT COUNT(*) 这类的计算是超快无比的。
InnoDB 的趋势会是一个非常复杂的存储引擎,对于一些小的应用,它会比 MyISAM 还慢。他是它支持“行锁” ,于是在写操作比较多的时候,会更优秀。并且,他还支持更多的高级应用,比如:事务。
mysql 数据库引擎: http://www.cnblogs.com/0201zcr/p/5296843.html MySQL存储引擎--MyISAM与InnoDB区别: https://segmentfault.com/a/1190000008227211
Docker
Docker 概念
docker面试题和解答 (opens new window)

Docker是一个容器化平台,它以容器的形式将您的应用程序及其所有依赖项打包在一起,以确保您的应用程序在任何环境中无缝运行。
Docker如何在非Linux系统中运行容器:
Docker for Mac和Windows都使用Linux VM来运行容器。Docker Toolbox用于在Virtual Box VM中运行容器。但是,最新的Docker在Windows中使用Hyper-V,在Mac中使用Hypervisor.framework。
什么是Docker镜像
Docker镜像是Docker容器的源代码,Docker镜像用于创建容器。使用build命令创建镜像。
什么是Docker容器
Docker容器包括应用程序及其所有依赖项,作为操作系统的独立进程运行。
容器中的资源管理:是通过cgroup实现的。
Docker容器有几种状态:
四种状态:运行、已暂停、重新启动、已退出。
Production
Kafka 原理
https://www.jianshu.com/p/0272d5e4ffad (opens new window) https://zhuanlan.zhihu.com/p/73259250 (opens new window)
常用命令
拉取或者更新指定镜像:
docker pull将镜像推送至远程仓库:
docker push删除容器:
docker rm删除镜像:
docker rmi列出所有镜像:
docker images列出所有容器:
docker ps连接到正在运行中的容器:
docker attach [OPTIONS] CONTAINER容器与主机之间的数据拷贝命令:
docker cp /www 96f7f14e99ab:/www/启动nginx容器(-P 随机端口映射),并挂载本地文件目录到容器html的命令
Docker run 命令 (opens new window)
docker run -d -p 80:8080 --name nginx2 -v /home/nginx:/usr/share/nginx/html nginxdocker迁移代码(保存、加载):
docker save -o <path for generated tar file> <image name>docker load -i <path to image tar file>
数据结构
1 红黑树
红黑树与AVL的比较:
AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多;
红黑是用非严格的平衡来换取增删节点时候旋转次数的降低;
所以简单说,如果你的应用中,搜索的次数远远大于插入和删除,那么选择AVL,如果搜索,插入删除次数几乎差不多,应该选择RB。
红黑树详解: https://xieguanglei.github.io/blog/post/red-black-tree.html
教你透彻了解红黑树: https://github.com/julycoding/The-Art-Of-Programming-By-July/blob/master/ebook/zh/03.01.md
2 B-Tree B+Tree
BTree和B+Tree (opens new window)
编程题
1 台阶问题/斐波那契
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
fib = lambda n: n if n <= 2 else fib(n - 1) + fib(n - 2)
第二种记忆方法
def memo(func):
cache = {}
def wrap(*args):
if args not in cache:
cache[args] = func(*args)
return cache[args]
return wrap
@memo
def fib(i):
if i < 2:
return 1
return fib(i-1) + fib(i-2)
第三种方法
def fib(n):
a, b = 0, 1
for _ in xrange(n):
a, b = b, a + b
return b
2 变态台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
fib = lambda n: n if n < 2 else 2 * fib(n - 1)
3 矩形覆盖
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
第
2*n个矩形的覆盖方法等于第2*(n-1)加上第2*(n-2)的方法。
f = lambda n: 1 if n < 2 else f(n - 1) + f(n - 2)
4 杨氏矩阵查找
在一个m行n列二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
使用Step-wise线性搜索。
def get_value(l, r, c):
return l[r][c]
def find(l, x):
m = len(l) - 1
n = len(l[0]) - 1
r = 0
c = n
while c >= 0 and r <= m:
value = get_value(l, r, c)
if value == x:
return True
elif value > x:
c = c - 1
elif value < x:
r = r + 1
return False
5 去除列表中的重复元素
用集合
list(set(l))
用字典
l1 = ['b','c','d','b','c','a','a']
l2 = {}.fromkeys(l1).keys()
print l2
用字典并保持顺序
l1 = ['b','c','d','b','c','a','a']
l2 = list(set(l1))
l2.sort(key=l1.index)
print l2
列表推导式
l1 = ['b','c','d','b','c','a','a']
l2 = []
[l2.append(i) for i in l1 if not i in l2]
sorted排序并且用列表推导式.
l = ['b','c','d','b','c','a','a'] [single.append(i) for i in sorted(l) if i not in single] print single
6 链表成对调换
1->2->3->4转换成2->1->4->3.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
# @param a ListNode
# @return a ListNode
def swapPairs(self, head):
if head != None and head.next != None:
next = head.next
head.next = self.swapPairs(next.next)
next.next = head
return next
return head
7 创建字典的方法
1 直接创建
dict = {'name':'earth', 'port':'80'}
2 工厂方法
items=[('name','earth'),('port','80')]
dict2=dict(items)
dict1=dict((['name','earth'],['port','80']))
3 fromkeys()方法
dict1={}.fromkeys(('x','y'),-1)
dict={'x':-1,'y':-1}
dict2={}.fromkeys(('x','y'))
dict2={'x':None, 'y':None}
8 合并两个有序列表
知乎远程面试要求编程
尾递归
def _recursion_merge_sort2(l1, l2, tmp):
if len(l1) == 0 or len(l2) == 0:
tmp.extend(l1)
tmp.extend(l2)
return tmp
else:
if l1[0] < l2[0]:
tmp.append(l1[0])
del l1[0]
else:
tmp.append(l2[0])
del l2[0]
return _recursion_merge_sort2(l1, l2, tmp)
def recursion_merge_sort2(l1, l2):
return _recursion_merge_sort2(l1, l2, [])
循环算法
思路:
定义一个新的空列表
比较两个列表的首个元素
小的就插入到新列表里
把已经插入新列表的元素从旧列表删除
直到两个旧列表有一个为空
再把旧列表加到新列表后面
def loop_merge_sort(l1, l2):
tmp = []
while len(l1) > 0 and len(l2) > 0:
if l1[0] < l2[0]:
tmp.append(l1[0])
del l1[0]
else:
tmp.append(l2[0])
del l2[0]
tmp.extend(l1)
tmp.extend(l2)
return tmp
pop弹出
a = [1,2,3,7]
b = [3,4,5]
def merge_sortedlist(a,b):
c = []
while a and b:
if a[0] >= b[0]:
c.append(b.pop(0))
else:
c.append(a.pop(0))
while a:
c.append(a.pop(0))
while b:
c.append(b.pop(0))
return c
print merge_sortedlist(a,b)
9 交叉链表求交点
其实思想可以按照从尾开始比较两个链表,如果相交,则从尾开始必然一致,只要从尾开始比较,直至不一致的地方即为交叉点,如图所示

# 使用a,b两个list来模拟链表,可以看出交叉点是 7这个节点
a = [1,2,3,7,9,1,5]
b = [4,5,7,9,1,5]
for i in range(1,min(len(a),len(b))):
if i==1 and (a[-1] != b[-1]):
print "No"
break
else:
if a[-i] != b[-i]:
print "交叉节点:",a[-i+1]
break
else:
pass
另外一种比较正规的方法,构造链表类
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def node(l1, l2):
length1, lenth2 = 0, 0
# 求两个链表长度
while l1.next:
l1 = l1.next
length1 += 1
while l2.next:
l2 = l2.next
length2 += 1
# 长的链表先走
if length1 > lenth2:
for _ in range(length1 - length2):
l1 = l1.next
else:
for _ in range(length2 - length1):
l2 = l2.next
while l1 and l2:
if l1.next == l2.next:
return l1.next
else:
l1 = l1.next
l2 = l2.next
修改了一下:
#coding:utf-8
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def node(l1, l2):
length1, length2 = 0, 0
# 求两个链表长度
while l1.next:
l1 = l1.next#尾节点
length1 += 1
while l2.next:
l2 = l2.next#尾节点
length2 += 1
#如果相交
if l1.next == l2.next:
# 长的链表先走
if length1 > length2:
for _ in range(length1 - length2):
l1 = l1.next
return l1#返回交点
else:
for _ in range(length2 - length1):
l2 = l2.next
return l2#返回交点
# 如果不相交
else:
return
思路: http://humaoli.blog.163.com/blog/static/13346651820141125102125995/
10 二分查找
#coding:utf-8
def binary_search(list, item):
low = 0
high = len(list) - 1
while low <= high:
mid = (high - low) / 2 + low # 避免(high + low) / 2溢出
guess = list[mid]
if guess > item:
high = mid - 1
elif guess < item:
low = mid + 1
else:
return mid
return None
mylist = [1,3,5,7,9]
print binary_search(mylist, 3)
参考: http://blog.csdn.net/u013205877/article/details/76411718
11 快排
#coding:utf-8
def quicksort(list):
if len(list)<2:
return list
else:
midpivot = list[0]
lessbeforemidpivot = [i for i in list[1:] if i<=midpivot]
biggerafterpivot = [i for i in list[1:] if i > midpivot]
finallylist = quicksort(lessbeforemidpivot)+[midpivot]+quicksort(biggerafterpivot)
return finallylist
print quicksort([2,4,6,7,1,2,5])
12 找零问题
#coding:utf-8
#values是硬币的面值values = [ 25, 21, 10, 5, 1]
#valuesCounts 钱币对应的种类数
#money 找出来的总钱数
#coinsUsed 对应于目前钱币总数i所使用的硬币数目
def coinChange(values,valuesCounts,money,coinsUsed):
#遍历出从1到money所有的钱数可能
for cents in range(1,money+1):
minCoins = cents
#把所有的硬币面值遍历出来和钱数做对比
for kind in range(0,valuesCounts):
if (values[kind] <= cents):
temp = coinsUsed[cents - values[kind]] +1
if (temp < minCoins):
minCoins = temp
coinsUsed[cents] = minCoins
print ('面值:{0}的最少硬币使用数为:{1}'.format(cents, coinsUsed[cents]))
思路: http://blog.csdn.net/wdxin1322/article/details/9501163
方法: http://www.cnblogs.com/ChenxofHit/archive/2011/03/18/1988431.html
13 广度遍历和深度遍历二叉树
给定一个数组,构建二叉树,并且按层次打印这个二叉树
14 二叉树节点
class Node(object):
def __init__(self, data, left=None, right=None):
self.data = data
self.left = left
self.right = right
tree = Node(1, Node(3, Node(7, Node(0)), Node(6)), Node(2, Node(5), Node(4)))
15 层次遍历
def lookup(root):
row = [root]
while row:
print(row)
row = [kid for item in row for kid in (item.left, item.right) if kid]
16 深度遍历
def deep(root):
if not root:
return
print root.data
deep(root.left)
deep(root.right)
if __name__ == '__main__':
lookup(tree)
deep(tree)
17 前中后序遍历
深度遍历改变顺序就OK了
#coding:utf-8
#二叉树的遍历
#简单的二叉树节点类
class Node(object):
def __init__(self,value,left,right):
self.value = value
self.left = left
self.right = right
#中序遍历:遍历左子树,访问当前节点,遍历右子树
def mid_travelsal(root):
if root.left is not None:
mid_travelsal(root.left)
#访问当前节点
print(root.value)
if root.right is not None:
mid_travelsal(root.right)
#前序遍历:访问当前节点,遍历左子树,遍历右子树
def pre_travelsal(root):
print (root.value)
if root.left is not None:
pre_travelsal(root.left)
if root.right is not None:
pre_travelsal(root.right)
#后续遍历:遍历左子树,遍历右子树,访问当前节点
def post_trvelsal(root):
if root.left is not None:
post_trvelsal(root.left)
if root.right is not None:
post_trvelsal(root.right)
print (root.value)
18 求最大树深
def maxDepth(root):
if not root:
return 0
return max(maxDepth(root.left), maxDepth(root.right)) + 1
19 求两棵树是否相同
def isSameTree(p, q):
if p == None and q == None:
return True
elif p and q :
return p.val == q.val and isSameTree(p.left,q.left) and isSameTree(p.right,q.right)
else :
return False
20 前序中序求后序
推荐: http://blog.csdn.net/hinyunsin/article/details/6315502
def rebuild(pre, center):
if not pre:
return
cur = Node(pre[0])
index = center.index(pre[0])
cur.left = rebuild(pre[1:index + 1], center[:index])
cur.right = rebuild(pre[index + 1:], center[index + 1:])
return cur
def deep(root):
if not root:
return
deep(root.left)
deep(root.right)
print root.data
21 单链表逆置
class Node(object):
def __init__(self, data=None, next=None):
self.data = data
self.next = next
link = Node(1, Node(2, Node(3, Node(4, Node(5, Node(6, Node(7, Node(8, Node(9)))))))))
def rev(link):
pre = link
cur = link.next
pre.next = None
while cur:
tmp = cur.next
cur.next = pre
pre = cur
cur = tmp
return pre
root = rev(link)
while root:
print root.data
root = root.next
思路: http://blog.csdn.net/feliciafay/article/details/6841115
方法: http://www.xuebuyuan.com/2066385.html?mobile=1
22 两个字符串是否是变位词
class Anagram:
"""
@:param s1: The first string
@:param s2: The second string
@:return true or false
"""
def Solution1(s1,s2):
alist = list(s2)
pos1 = 0
stillOK = True
while pos1 < len(s1) and stillOK:
pos2 = 0
found = False
while pos2 < len(alist) and not found:
if s1[pos1] == alist[pos2]:
found = True
else:
pos2 = pos2 + 1
if found:
alist[pos2] = None
else:
stillOK = False
pos1 = pos1 + 1
return stillOK
print(Solution1('abcd','dcba'))
def Solution2(s1,s2):
alist1 = list(s1)
alist2 = list(s2)
alist1.sort()
alist2.sort()
pos = 0
matches = True
while pos < len(s1) and matches:
if alist1[pos] == alist2[pos]:
pos = pos + 1
else:
matches = False
return matches
print(Solution2('abcde','edcbg'))
def Solution3(s1,s2):
c1 = [0]*26
c2 = [0]*26
for i in range(len(s1)):
pos = ord(s1[i])-ord('a')
c1[pos] = c1[pos] + 1
for i in range(len(s2)):
pos = ord(s2[i])-ord('a')
c2[pos] = c2[pos] + 1
j = 0
stillOK = True
while j<26 and stillOK:
if c1[j] == c2[j]:
j = j + 1
else:
stillOK = False
return stillOK
print(Solution3('apple','pleap'))
